Тема: Куб разности двух выражений
|
Жетписова Айгуль Естаевна, учитель математики, первая квалификационная категория высшего уровня, КГУ «Александровская основная школа» СКО Есильский район, село Александровка |
 |
Тип урока: урок совершенствования знаний, умений, навыков.
Цели урока:
- повторение формул сокращенного умножения, формирование умения геометрически интерпретировать формулу куба разности двух выражений,
- развитие пространственного воображения, логического мышления,
- воспитание любознательности, аккуратности.
Методы: создание проблемной ситуации, наглядный.
Оборудование: угольник, плотная бумага, ножницы, модели кубов, прямоугольных параллелепипедов.
Ход урока:
1. Организационный момент.
2. Проверка выполнения домашнего задания.
3. Актуализация опорных знаний: повторение формул:
V=a3 (формула объем куба);
V=a*b*c (формула объема прямоугольного параллелепипеда);
(a+b)3=a3+3a2b+3ab2+b3 (куб суммы двух выражений);
(a-b)3=a3-3a2b+3ab2-b3 (куб разности двух выражений).
4. Задание. Дан куб с ребром а, уменьшить сторону куба на b единиц. Найти объем куба с ребром а-b, т. е. (a-b)3. Построить чертеж.
Преобразуем формулу куба разности (a-b)3=a3-3a2b+3ab2-b3 =a3-3ab(a-b)-b3
Чтобы получить куб со стороной а-b можно от объема куба со стороной а отнять утроенный объем прямоугольного параллелепипеда со сторонами а, b, a-b, и отнять объем куба со стороной b.
Выполнение соответствующего чертежа.
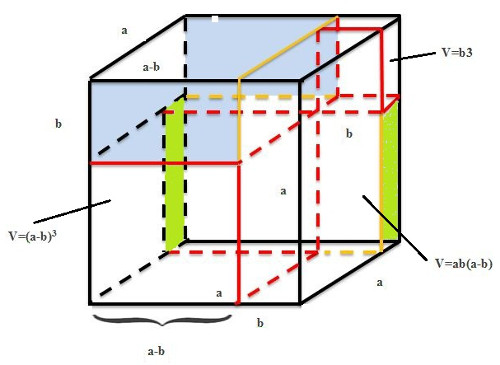
Рисунок 1. Построение чертежа по формуле куба разности
5. Изготовление соответствующих моделей двух кубов и трех параллелепипедов.
6. Подведение итогов урока.
7. Рефлексия.
- 7914 просмотров


.webp)





.webp)
