КВН
|
Маштиева Баян Зиядиновна учитель математики и информатики І категория ГУ Аккольская средняя школа Зерендинского района Акмолинской области |
 |
Цель: Воспитание интереса к предмету; чувства сопереживания за свою команду, развитие смекалки, творчества, уважения друг другу
Подготовка: заранее команды готовят название, девиз, эмблему, выбирают капитана
Оборудование: интерактивная доска, бумага, ручки, маркеры, ромашка, палочки, грамоты
Класс красочно оформлен. Плакаты у болельщиков. Звучит музыка
Программа: КВН состоит из 7 конкурсов
Ведущий: Добрый день друзья! Мы приветствуем всех собравшихся в зале. Зал полон самыми веселыми и находчивыми ребятами. Поэтому мы проведем среди таких ребят состязание. Итак, внимание! На сцену приглашаются команды:
В нашем зале находится жюри, которое будет оценивать наш конкурс
І конкурс. Приветствие команд «Знакомьтесь, это мы!» /максимальный балл — 5 баллов/
ІІ конкурс. Разминка /оценивается по 1 баллу на каждый правильный ответ/
1. Горело 5 свечей, 4 погасли. Сколько осталось? /4/
2. Какой знак надо поставить между 0 и 1, так чтобы получилось число больше 0, но меньше 1? /,/
3. Назовите имя, отчество и фамилию русской женщины — математика /
4. Летела стая сов семь не большая. Какие птицы и сколько их было? / 7 сов/
5. В каком году была изобретена первая электрическая лампочка накаливания, если от начала летоисчисления до этого года прошло полных 1872 года? /1873 г./
6. Айгуль и Сания сестры, Айгуль сказала, что у нее тоже 2 брата. Сколько детей в семье? /4/
7. Какую математическую задачу решает свинья, когда подрывает куст картофеля? / ищет корни/
8. В каком месяце встречается число 28? / во всех /
9. Может ли в одном месяце быть 5 выходных? /да/
10. Вычислите произведение целых чисел от — 99 до 99. /0/
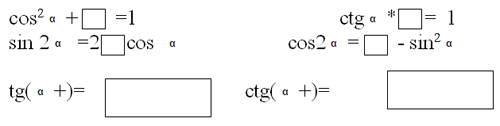
ІІІ конкурс. Игра «Закрой форточку» / по 3 балла/ В формулах тригонометрических тождеств допишите не достающиеся звенья
IV конкурс. Конкурс капитанов /5 баллов/
а/ На доске появляется слайд с рисунком Ромашки, на каждом лепестке размещена буква. Задание: Капитаны поочередно на каждую букву называют математический термин с определениями.

б/ Решите задачу
Лошадь съедает стог сена за 2 дня, корова за 3, овца за 6. Сколько дней они съедают стог, если будут есть его вместе? / 1 день /
Игра с болельщиками /1 балл/
Болельщики, заработанный балл могут отдать своей болеющей команде.
1. Над рекой летели птицы, —
Голубь, щука, две синицы,
Два стрижа и пять угрей.
Сколько птиц ответь скорей? /5/
2. Черненькая, хвостатенькая
Не лает, не кусает,
А из класса не пускает. /двойка/
3. Что больше: а или 2а? /если, а — положительное число, то 2а, иначе а/
4. На что похожа половина апельсина? /на другую половину /
V конкурс. Исторические задачи. Каждой команде по 1 задаче /5 баллов/
1. Дружественные числа — это два натуральных числа, для которых сумма всех делителей первого числа (кроме него самого) равна второму числу и, в свою очередь, сумма всех делителей второго числа (кроме него самого) равна первому числу. Всегда, когда говорят о дружественных числах, то имеют в виду пары числе. Таким образом, эти числа связаны отношениями сходства и поэтому были названы дружественными. Впервые дружественные числа упоминаются в работах Пифагора, посвященных теории чисел. Следует отметить, что пифагорейцам была известна лишь одна пара дружественных чисел 220 и *** . Долгое время эта пара чисел была единственным представителем класса дружественных чисел. Найдите дружественное ему число?/
2.В книге «Начал» Евклид доказал, что если число 2 n — 1простое, то число 2
28= 23–1(23–1)=4*7=28
496=25–1(25–1)=16*31=496
VI конкурс. «Римские цифры» /2 балла/ Несколько числовых равенств с римскими цифрами, сложенных из палочек. Задание: В каждом равенстве одна палочка лежит не на своем месте. Найдите и исправьте ошибки.
VI+I=V X+III=XI
VII конкурс. «Музыкальный» /по 1 баллу за песню / Команды поют по 3–4 строчки из песен, где встречаются числа.
— Дорогие ребята! на такой веселой ноте хочется закончит наш конкурс. Вот и подошел к концу наш КВН. Пусть жюри огласит победителей.
Итоги.
Поздравления.
Награждения.
- 11200 просмотров