Математика сабағында проценттік құрамға және концентрацияға есептер шығару
|
Оңтүстік Қазақстан облысы Төлеби ауданы Б.Момышұлы атындғы жалпы орта мектеп математика пәнініңмұғалімі: Муратбекова С.К. |
 |
Концентрацияға және проценттік құрамдарға берілген есептер жалпы білім беретін мектеп оқушыларына ол есептермен алғашқы танысу барысында көптеген қиындықтар туғызады. Ол есептерді өздігінен шешу көп оқушылардың қолынан келе бермейді. Тәжірибелік маңызы зор болып келетін бұл есептер оқушылардың ойлау қабілетін дамытуда көп септігін тигізетіні сөзсіз. Оның үстіне бұл тақырыпқа арналған есептер ҰБТ тесттерінде-де көп кездеседі.
Бұл есептерді бірнеше жолмен шығаруға болады. Бұл әдістемелік нұсқауда сол әдістерге шолу жасап көрдім. Төменде осындай есептерді 4 тәсілмен шығару жолдарын ұсынып отырмын.
I. Аналитикалық тәсілмен шығару
1. Теңіз суында 5% тұз бар. Массасы 80кг болатын теңіз суынан 4% тұзды су алу үшін қанша кг тущы су қую керек?
х кг - ІІ ерітіндідегі тұщы судың массы
у кг - І ерітіндідегі тұздың массасы
Пропорция құрамыз
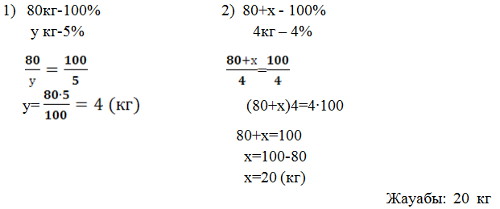
II. Таблица құру әдісі
Мысал 2: Массалары 80 гр және 120 гр екі тұз ерітіндісі бар. Бірінші ерітіндіде 12 гр, ал екінші ерітіндіде 15 гр тұз бар. Екі ерітіндіні қосқанда пайда болатын ерітіндіндідегі тұздың концентрациясын анықтаңыз.
Шешуі: Мұндағы белгісіз үшінші ерітіндіндідегі тұздың концентрациясы — x%.
Таза зат — тұз.
| Қоспаның күйі |
Қоспаның, ерітіндінің массасы M |
Массалық концентрациясы Ca |
Таза заттың массасы ma=M*Ca |
| I-ші ерітінді | 80 | 0,15 | 12 |
| II-ші ерітінді | 120 | 0,125 | 15 |
| I+II | 80+120=200 | х | 12+15=27 |
Берілген таблица арқылы теңдеу құрамыз:
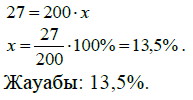
III. Диагональдік әдіс (Пирсон конверті)
Келесі белгілеулерді енгізейік:
w1 — 1-ші ерітіндіде ерітілген заттың массалық үлесі;
w2 — 2-ші ерітіндіде ерітілген заттың массалық үлесі;
w — 1-ші және 2-ші ерітіндіні араластырғанда пайда болған ерітіндіндідегі заттың массалық үлесі;
m1 — 1-ші ерітіндінің массасы;
m2 — 2-ші ерітіндінің массасы;

IV. Ескі тәсіл
Ескі тәсілмен есепті теңдеу құрмай-ақ тез шығаруға болады. Ол
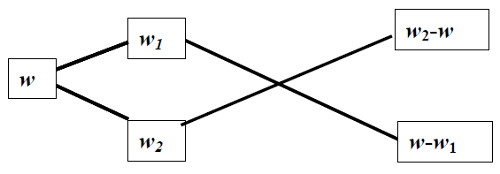
Бұл схема балыққа ұқсағандықтан бұл тәсілді кейде «балық» тәсілі деп те атайды. Бұл тәсілде w1 <w<w2 болуы шарт емес, тек үлкенінен кішісін алып тастау қажет. Ресейде алғашқы рет бұл тәсіл 18 ғасырдың арифметикасында кездеседі. Ол кітаптың авторы Леонтий Филиппович Магницкий (1669–1739) болғандықтан ол арифметика «Магницкий арифметикасы» деп аталған. Бұл оқулықты М. В. Ломоносов «білімпаздық қақпасы» деп атаған.
Мысал 4. Дүкенде шәйдің 3 сорты бар — 1 фунтының бағасы 5 гривен тұратын цейлон шәйі, 8 гривен тұратын үнді шәйі және 12 гривен тұратын қытай шәйі. Сатушы 1 фунтының бағасы 6 гривен болатын шәй алу үшін осы берліген 3 сортты шәйді қандай қатынаста алуы қажет? Шешуі: Бұл есепті шығару үшін схеманы екі рет қолданамыз: бірінші схемада бағалары ең жоғары және ең кіші шәй сорттарын аламыз, ал екінші схемада бағалары орта және ең кіші шәй сорттарын аламыз.
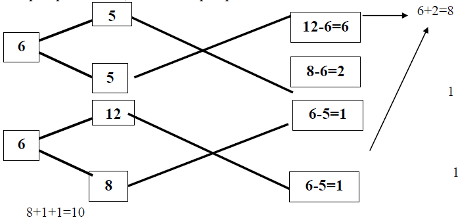
Жауабы: Демек цейлон шәйінен 8/10 кг, үнді шәйінен 1/10 кг және қытай шәйінен 1/10 кг алу қажет.
Пайданылған әдебиеттер
- 5 сынып Математика Алдамуратова Г. А. Атамұра 2005 ж.
- Анарбекова Ә. Бейсеков Ж., Алгебра сабақтарында қиын есептер шығару 2009 ж.
- Бейсеков Ж. жоғары оқу орындарға түсуші талапкерлерге арналған әдестемелік құрал 2010 ж.
- И. С. Слонимская, Л. И. Слонимский Математика «Решение текстовых задач».
- https://1september.ru//
- Сборник текстовых заданий по математике за 2003—2006 гг., 2009, 2010, 2011, 2012
- Я. Л. Гольдфараб Сборник задач «Упражнений по химии»
- О. В. Борздун. Основные методы решение задач по смешавание растворов.
- М. Н. Кочагина; В.В Кочагин Математика 9 Москва 2008
- Кузнецова и др. Зборник задач по подготовие «ГИА» 2011
- В. А. Далингер текстовые задачи, решение методом составление упражнений ОмТПЧ 1996
- 36020 просмотров