Метод математического моделирования в регулировании социально-экономических процессов
|
Шайхутдинова Альфия Фауисовна, учитель математики, |
 |
Задача о снижении веса спортсмена для восстановления весовой категории
Задача
Мой брат боксер, и через месяц должны были состояться отборочные турниры для поездки в Астану для участия в первенстве Вузов РК. Предстояли тренировки, взвешивания. Оказалось его вес на этот момент стал 71 кг (это
Постановка задачи — первый и наиболее важный этап построения модели, способный обеспечить правильное решение проблемы.
Спортсмену необходимо похудеть, за помощью обратились к «математике»
Построение модели — рассмотрение этого этапа и является главной целью.
Знакомые посоветовали перейти на питание, состоящее из двух продуктов W и R. Чтобы похудеть, в сутки этими продуктами надо получать 14 единиц жира, но не менее 300 калорий. На упаковке продукта W написано, что 1 кг этого продукта содержится 15 ед. жира и 150 калорий, а на упаковке продукта R — 4 единицы жира и 200 калорий соответственно. При этом цена 1 килограмма продукта W равна 150 тенге., а 1 кг продукта R — 250 тенге. Запишем это в виде таблицы:
|
Продукт |
Содержание жира в 1 кг |
Калорийность 1 кг |
Количество продукта, необходимое для диеты |
Цена за 1 кг |
|
Продукт W |
15 ед.жира |
150 кал. |
х |
150 тг |
|
Продукт R |
4 ед.жира |
200 кал. |
у |
250 тг. |
Так как брат жил в другом городе на стипендию, он был стеснен в средствах, но его интересовал вопрос: в какой пропорции нужно брать эти продукты для того, чтобы выдержать условия диеты и истратить как можно меньше денег?
Перейдем к формализации данной ситуации на языке математических символов.
Обозначим необходимые для выполнения условий диеты количества:
х — количество продукта, тогда количество ед.жира — 15х
у — количество продукта, тогда количество ед.жира — 4у
Количество ед. жира в (W + R) = 15х + 4у и по условию не превосходит 14: 15х + 4у < 14 необходимые для выполнения условий диеты.
Количество калорий, содержащихся в х кг W и в у кг R, равно 150х + 200у и по условию диеты должно быть не меньше 300: 150×200y < 300
Теперь о стоимости z продуктов. z 150×250y и в соответствии с высказанными пожеланиями должна быть минимальной.
Последнее записывается так:
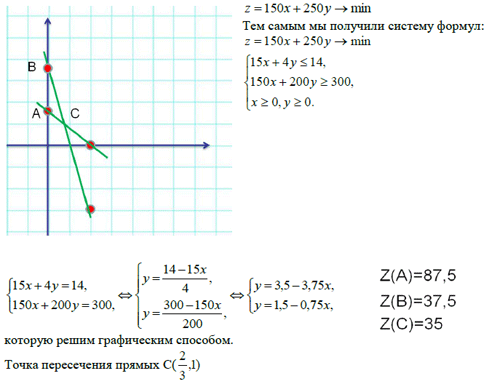
Нас интересует только та ее часть, которая лежит над треугольником АВС. Вычисляя значения z во всех трех вершинах этого треугольника zB=37,5 zA= 87,5 zC= 35 и сравнивая полученные результаты, замечаем, что наименьшее значение (z=35) достигается в вершине С.
Таким образом,

и искомая пропорция →2 : 3. Значит продукты нужно брать в отношении 2 W : 3 R, чтобы выдержать условия диеты и истратить как можно меньше денег.
Спортсмен выполнил эти условия и в результате его вес по истечении месяца снизился на 2 кг 700 г при активной физической подготовке.
Список использованной литературы:
- Райниц
В. Я. Модели планирования уровня жизни. — М.: Экономика, 1978. - Канторович Л.В., Гортско
А. Б. Оптимальные решения в экономике. М., «Наука», 1972.
- 8183 просмотра